Introducción a las expresiones algebraicas

Uno de los procedimientos algebraicos importantes estamos llamados a hacer es evaluar expresiones. Eso significa que la reducción de la expresión de un valor numérico, o su forma simplificada. Evaluación de expresiones no siempre es sencilla. Hay una manera sistemática para evaluar expresiones para asegurarse de obtener la respuesta correcta. Si se le da una expresión que contiene una variedad de diferentes operaciones, hay un orden específico en el que se deben realizar estas operaciones. Esta orden se llama el orden de las operaciones.

En esta unidad, vamos a revisar la notación, los conceptos y procedimientos necesarios para la evaluación de expresiones. Ya que es fundamental para entender los exponentes con el fin de entender los procedimientos posteriores, vamos a empezar por ahí. Vamos a seguir con la multiplicación, división, suma y resta de términos algebraicos, y luego discutir el uso de paréntesis y otros símbolos de agrupación. A continuación, se aplicará lo siguiente lo revisamos el orden de operaciones.

Exponentes

La notación exponencial

Se encuentra comúnmente en términos algebraicos, expresiones y ecuaciones. exponentes se utilizan para acortar o condensar multiplicación repetida. Por ejemplo, se muestra un término que contiene un exponente a continuación:

En este caso, 3 es la base de y 4 es el exponente. El exponente o potencia, indica el número de veces que el factor, o de base, se multiplica.

Cuando se trabaja con expresiones que contengan sólo números, sólo tiene que llevar a cabo la multiplicación indicada. A continuación se presentan tres ejemplos:

Ejemplo 1

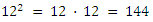
Ejemplo 2

Ejemplo 3

Observe en el segundo ejemplo de que un número elevado a la primera potencia es sólo ese número    (4 ^1 = 4). Cuando ves a un número que no tiene exponente, es porque se supone que el 1. Cuando se incluyen las variables de la relación, trabajamos de acuerdo a los mismos principios.

Exponentes en Álgebra

Exponentes incluidos en los términos y expresiones algebraicas pueden aplicarse a una sola variable a todo un término, o a una expresión. Cuando un término o expresión se eleva a una potencia, tenemos que aplicar el exponente de todo el término o conjunto de términos.

Una variable elevada a una potencia

Si el término no es más que una variable, el exponente se maneja igual a lo que vimos  en la parte anterior. Si queremos elevar un número o variable a una potencia, ponemos el exponente como un exponente de que un número o variable. A continuación se muestra una expresión algebraica que contiene un exponente.

Ejemplo 1

Ejemplo 2

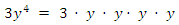
Al igual que con los números, una variable que no tiene una potencia es igual a la variable con potencia uno.

Un término elevado a una potencia

Recuerde que un término es un número o un producto de un número de una o más variables. Esto incluye cualquier potencia a las que se elevan las variables. En un término o en un conjunto términos, o simplemente una variable dentro de un término, que pueden elevarse a una potencia. Para indicar que todo el término se eleva a una potencia, hay que incluir en el término paréntesis y colocar el exponente fuera del paréntesis. La regla general para la aplicar exponente a todo un término indica que el término tiene que estar contenido entre paréntesis y es:

El resultado es muy diferente que cuando se omiten los paréntesis.

Ejemplo 1

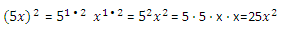
Con paréntesis

Ejemplo 2

Sin paréntesis

Multiplicando dos términos con la misma variable

A veces debemos multiplicar dos variables juntas que tienen diferente exponente. Cuando se multiplican este tipo de términos, se agregan los exponentes de cada una de las variables.

Ejemplo 1

Al principio tal vez no quede claro. Pero mira los siguientes ejemplos.

Ejemplo 2

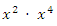
Son dos variables con diferentes potencias.

Ejemplo 3

Si multiplicamos estas dos variables tenemos: