
Definición
En matemáticas, el límite es un concepto que describe la tendencia de una sucesión o una función, a medida que los parámetros de esa sucesión o función se acercan a determinado valor. En cálculo (especialmente en análisis real y matemático) este concepto se utiliza para definir los conceptos fundamentales de convergencia, continuidad, derivación, integración, entre otros.Es decir que una función f(x), se acerca a el número L a medida que "x" tiende o se acerca al numero "a" ya sea por la derecha o la izquierda, este no necesariamente llega a toparlo.
Para que Lim x->a f(x) existan, es necesario que los límites por la izquierda y la derecha existan y deben ser iguales.
Limites Indeterminados
Son indeterminaciones todas aquellas expresiones en las que, al sustituir en ellas "x" por el valor al que tiende a las siguientes expresiones matemáticas:

Tipos de Indeterminaciones
Este tipo de limite se resuelve realizando operaciones indicadas

Ejercicio 1:
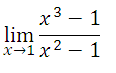
Remplazando “x”

Salvando indeterminación

En casos donde sobre todo aparecen raíz, basta con solo multiplicar y dividir por la conjugada de la raíz. Utilizamos la igualdad notable suma por la diferencia para conseguir quitar la raíz.

Ejercicio 2:
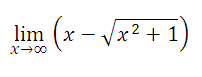
Remplazando “x”

Salvando indeterminación


(nota:un numero sobre infinito es igual a cero)
Este tipo de limite se resuelve realizando operaciones indicadas.

Ejercicio 3:

Remplazando “x”

Salvando indeterminación

En la mayoría de los casos basta con solo dividir el numerador y el denominador por la mayor potencia de "x" del denominador.
(nota:un numero sobre infinito es igual a cero)

Ejercicio 4:

Remplazando “x”

Salvando indeterminación

Las siguientes indeterminaciones

Se pueden resolver utilizando la siguiente expresión
Donde resulta
Pudiendo aparecer otras indeterminaciones, que resuelven por otros métodos anterior mente propuestos.






